Mittwoch, 29. August 2007
Beugung
Es gibt Phänomene in einigen Bereichen der Physik, die sich geometrisch nicht erklären lassen. Ein einfaches Beispiel ist, wenn eine Wasserwelle eine Hafeneinfahrt erreicht. Dann entsteht in der Hafeneinfahrt, wenn diese sehr schmal ist, eine Welle, die aussieht, als wäre in der Einfahrt ein Stein ins Wasser geworfen worden. Sie können die Welle an Stellen im Hafen sehen, von denen aus Sie das Schiff, das sie verursacht hat, nicht sehen können.
Ähnlich ist es auch mit dem Licht. Wenn Sie sich das Licht als Teilchen vorstellen, das in Richtung auf die Blende einer Kamera abgeschossen wird, dann sollte sich das Licht geradlinig ausbreiten und hinter der Blende auf den Sensor treffen. Das ist aber nicht der Fall. Das Licht fällt auch in Bereiche, an denen man es nicht finden dürfte, wenn es ein Teilchen wäre, das durch das Objektiv fliegt. Auch bei dem besten Objektiv entsteht deshalb ein so genanntes Beugungsscheibchen, das um so breiter ist, je kleiner die Blende wird.
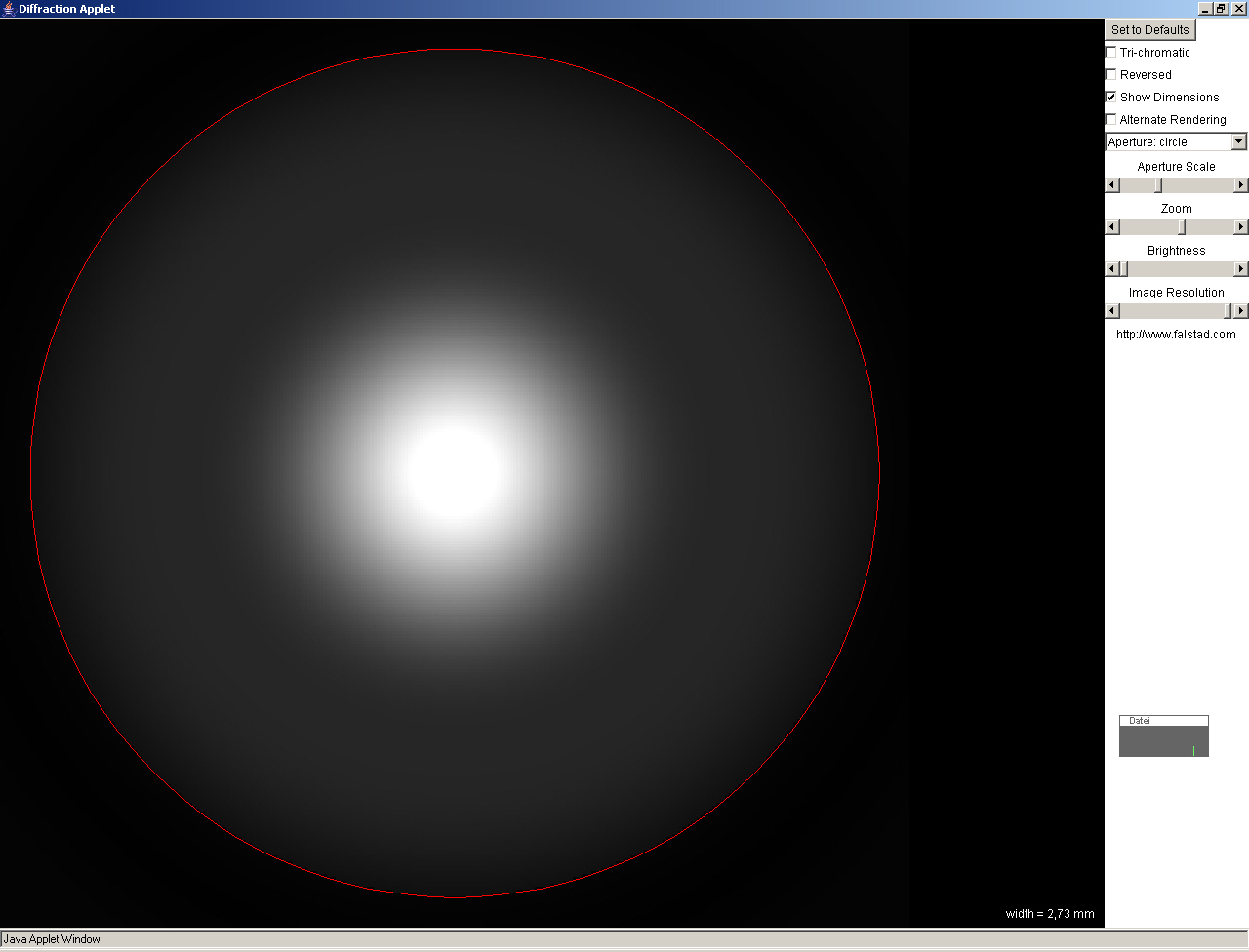
Das Beugungsbild zeigt ein helles Zentrum, das von hellen und dunklen Ringen umgeben ist, wobei die Helligkeit nach außen hin schnell abnimmt.
Der Radius des Beugungsscheibchens bzw. des hellen Zentrums berechnet sich aus:
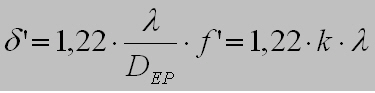
mit
d’= Radius des Beugungsscheibchens
lambda = Lichtwellenlänge
DEP= Durchmesser der Eintrittspupille
K= Blendenzahl
Je größer die Blendenzahl, desto größer das Beugungs- oder Airy-Scheibchen. Die Frage, die sich nun stellt ist: „Ab wann wird die Beugung zum begrenzenden Faktor für die Detailwiedergabe, also die Auflösung?“ Dazu ist zunächst einmal zu betrachten, ab wann der Mensch die Beugungsscheibchen als getrennte Punkte wahrnimmt. Diese Untersuchung wurde 1879 von Lord Rayleigh durchgeführt und veröffentlicht. Sie zeigt, dass die Intensität des Bereiches zwischen 2 Airy-Scheibchen auf 81% der Maximalintensität abgefallen sein muss, damit die Scheibchen mit dem Auge als getrennt wahrgenommen werden können. Dieses ist genau dann der Fall, wenn die Maxima der Beugungsscheibchen einen Abstand haben, der dem Radius eines Scheibchens entspricht.
Auf die Pixel einer digitalen Kamera übertragen sollte der Radius des Beugungsscheibchens kleiner sein, als der Abstand zwischen 2 Pixeln. Um die Größe des zulässigen Beugungsscheibchens und daraus dann weiterführend die kleinste Blende bei der die Beugung die Auflösung noch nicht begrenzt zu bestimmen, müssen wir also die Größe des Pixels der jeweiligen Kamera kennen. Hierzu kann einfach die Sensorbreite durch die Anzahl an Pixel geteilt werden und man erhält die Größe für 1 Pixel.
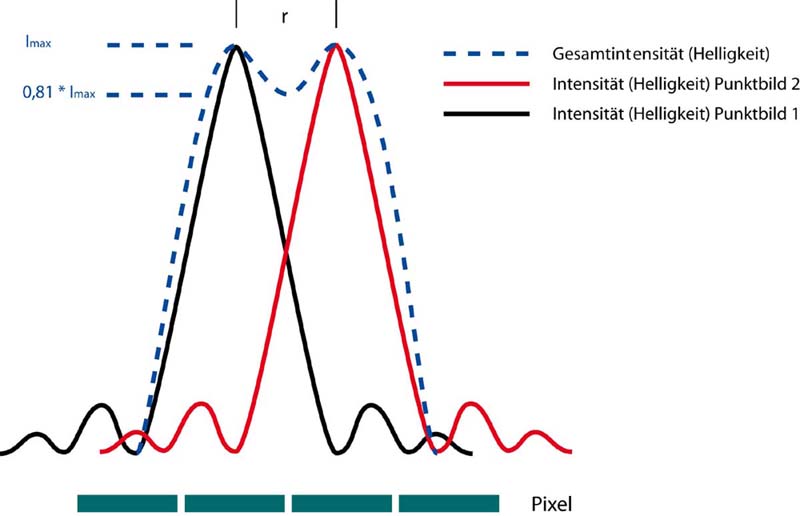
Die Beugungsfigur von zwei Punkten. Wenn sie einen Abstand haben, der dem Radius entspricht, dann können sie mit dem Auge bei hinreichender Vergrößerung gerade noch als getrennt wahrgenommen werden.
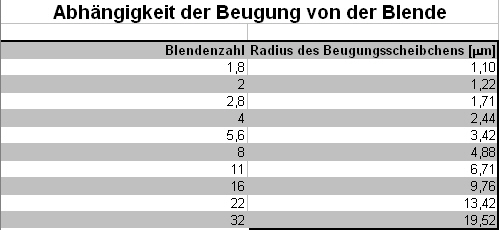
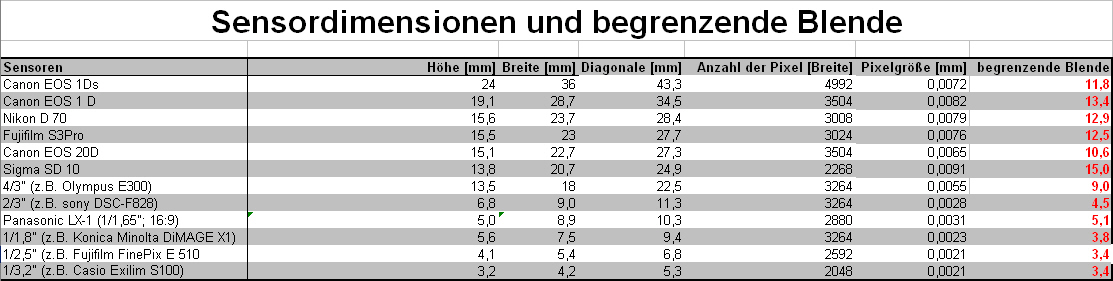
Die Tabelle gibt für die aufgeführten Kameras die begrenzende Blende (rechte Spalte) an. Bei kleineren Blenden (größere Blendenzahlen) begrenzt die Beugung das Auflösungsvermögen der Kamera.
Wie die Tabelle mit der begrenzenden Blende zeigt, beginnt bei den digitalen SLRs die Auflösungsbegrenzung durch Beugung in der Regel ca. ab Blende 11. Bei Konsumerkameras kann bereits ab Blende 4 ein sichtbarer Auflösungsverlust eintreten.
Unsere Beispielbilder von der Panasonic LX-1 zeigen, dass bereits bei Blende 5,6 eine sichtbare Verschlechterung der Auflösung eintritt.

Die Bilder zeigen jeweils das Zentrum unseres Auflösungstestbildes, aufgenommen mit einer Panasonic LX-1 bei einer Blende von 4, 5,6 und 8 (v. l.). Es zeigt sich, dass bereits bei Blende 5,6 die Auflösung bedingt durch Beugung sichtbar schlechter wird.
Fazit
In Bezug auf die Beugung haben Digitalkameras mit großen Pixeln Vorteile, weil auch kleinere Blenden bis Blende 11 verwendet werden können, ohne, dass die Auflösung schlechter wird. Die großen Pixel sind in der Regel in digitalen Spiegelreflexsystemen mit großen Sensoren zu finden. Bei Consumerkameras mit kleinen Pixeln ist darauf zu achten, dass nicht zu weit abgeblendet wird, weil die Auflösung sonst sichtbar leidet. Hinsichtlich der Schärfentiefe spielt die Beugung nur eine untergeordnete Rolle, weil mit kleinem Sensor zwar die begrenzende Blende größer wird, die Schärfentiefe aber auf der anderen Seite zunimmt (siehe Color Foto Heft 9/2005 Seite 51f).
Datenmenge
Pixelanzahl
[Megapixel] | Dateigröße*
unkomprimiert | JPEG-Dateigröße*
(hohe Qualität)
komprimiert |
|---|
| 2 | 6 MB | ca. 1.2 MB |
| 6 | 18 MB | ca. 2.4 MB |
| 8 | 24 MB | ca. 4.8 MB |
| 10 | 30 MB | ca. 6.4 MB |
| 12 | 36 MB | ca. 7.2 MB |
* Sofern die Detailwiedergabe der Kamera den theoretischen Vorlagen entspricht (hervorragendes Objektiv, etc.)
Für jedes Pixel braucht man, um Farben korrekt darstellen zu können, 3 Byte – 1 Byte für jede Farbe Rot, Grün und Blau.
Das JPEG-Format trennt die Farben eines Bildes in seine Helligkeitsinformation (die Zeichnung und die Details eines Bildes) und zwei Farbsignale. Es speichert einen Großteil der Farbinformation nicht und fasst die Informationen so gut es geht und je nach eingestellter Qualität zusammen (Kompression). Dabei geht Information verloren, wobei die Qualität von nicht sichtbarem Verlust (selbst bei stärkster Vergrößerung) bis hin zu unbrauchbarem Bild reicht.
Die Datenmenge einer Bilddatei sollte man im eigenen Interesse möglichst gering halten, denn viel Information nimmt viel Speicherplatz in Anspruch. Trägt die Bilddatei zu viele Informationen, die z.B. durch eine hohe Pixelanzahl oder durch eine hoch eingestellte Bildqualität verursacht wird, verlangsamen sich nachfolgende Prozesse wie beispielsweise die Benutzung von Bildbearbeitungsprogrammen, die Bilddatenübertragung z.B. via Email oder das einfache Laden/ Öffnen der Dateien.
Zusammengefasst gilt also: Je mehr Pixel, desto größer die Datei;
und deswegen: So viel wie nötig, aber so wenig wie möglich.
Aus http://6mpixel.org/beugung/





























 Dies ist eine mit page4 erstellte kostenlose Webseite. Gestalte deine Eigene auf www.page4.com
Dies ist eine mit page4 erstellte kostenlose Webseite. Gestalte deine Eigene auf www.page4.com